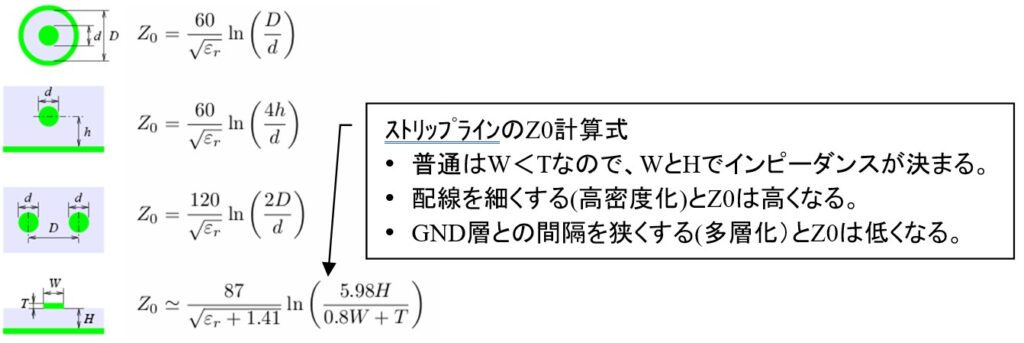
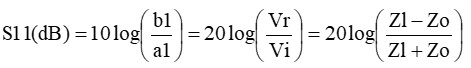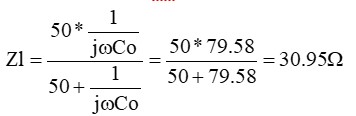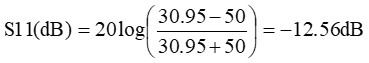だいぶ時間が空いてしまいましたが、PLLのその5を書きたいと思います。
ビヘイビアモデルをつかう
応答速度とジッタの量の関係を確認する
今回は、ビヘイビアモデルを使って応答速度とジッタの量の関係を確認してみたいと思います。
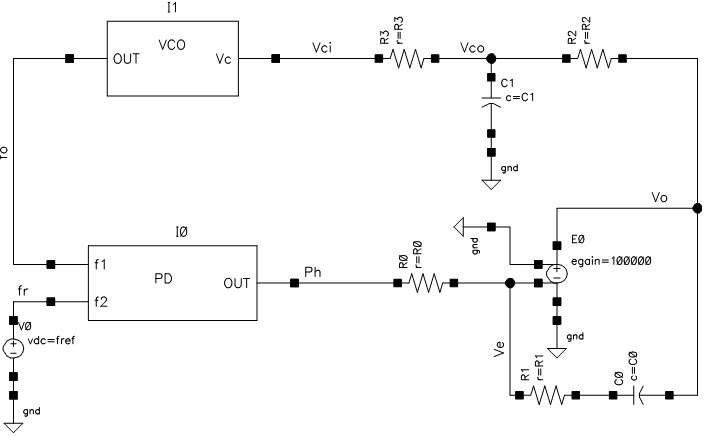
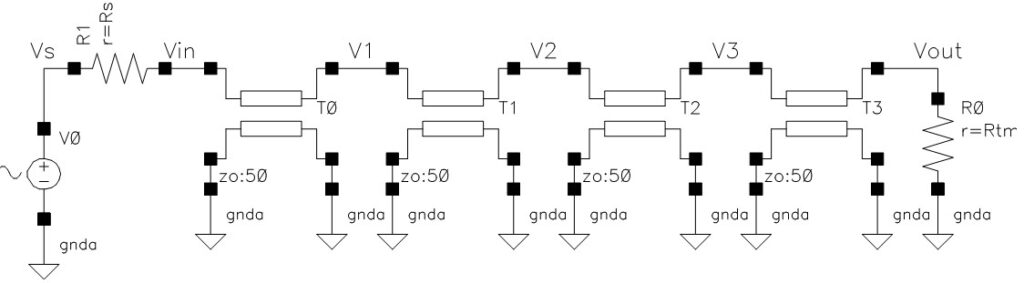
図 1にビヘイビアモデルを使ってPLL全体の回路を示します。(PLLその2-PLLその3で使って物を同じです)
まずはノイズ源ですが・・・VCOの制御電圧に意図的に雑音源を入れました。
evco out 0 value=fo*(2/(exp((Vref-v(vcn))/Kv)+1))
vnoise vcn vc noise fmin=10 fmax=10MEG THN=0.01n
1行目はVCOの入出力(制御電圧=>出力周波数)特性を計算式で書いたもので、使ったパラメータは下記の値です。
.param fo=100
.param dfp=’5/3.3′
.param Kv=’1/(2*dfp)’
.param Vref=1.65
.param fref=100
2行目が雑音源になります。VCO外部からの制御電圧Vcに雑音を加味してVcnとし、この電圧がVCOの発振周波数を決めるようにしています。雑音は10Hzから10MHzの熱雑音(白色雑音)で、0.01nV2/Hzの大きさです。
固定電圧を与えてPLL=OPENで過渡解析を行う
この状態で、PLLをOPENにして(VCO入力のR3を外して)Vciに固定電圧をあたえて雑音を含めた過渡解析を行った結果どうなるかと言うと、次のようになります。
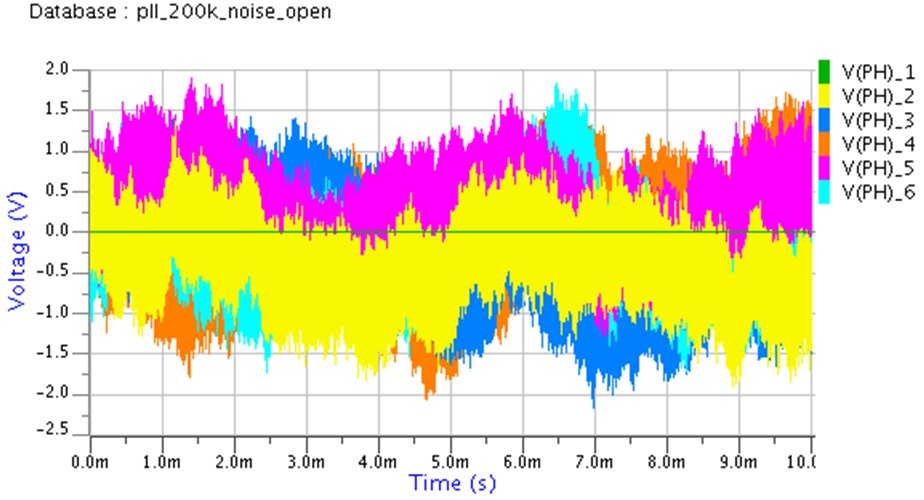
位相比較器の出力電圧は、雑音が無い時(V(PH)_1)に対して±1周期以上ずれていて、ゆらゆらしていることが分かります(V(PH)_2~6は雑音を考慮した過渡解析結果です)。
つまり、ジッタが1周期を超えてしまっている上に安定していないと言っていて、このままでは全く使い物になりません。これはPLLをOPENにした結果なので、VCOを単体で使うとこうなってしまいます。(発振器にクリスタルを使ったVCXOやTCXOなどは格段に安定しているので、こうはなりません)
PLL=CLOSEで応答速度毎にジッタの変化を見る
それでは、PLLをCLOSEにしてみたいと思います。
CLOSEする際、PLLの応答速度はフィルタ定数などを変更して下の3種類にしました。
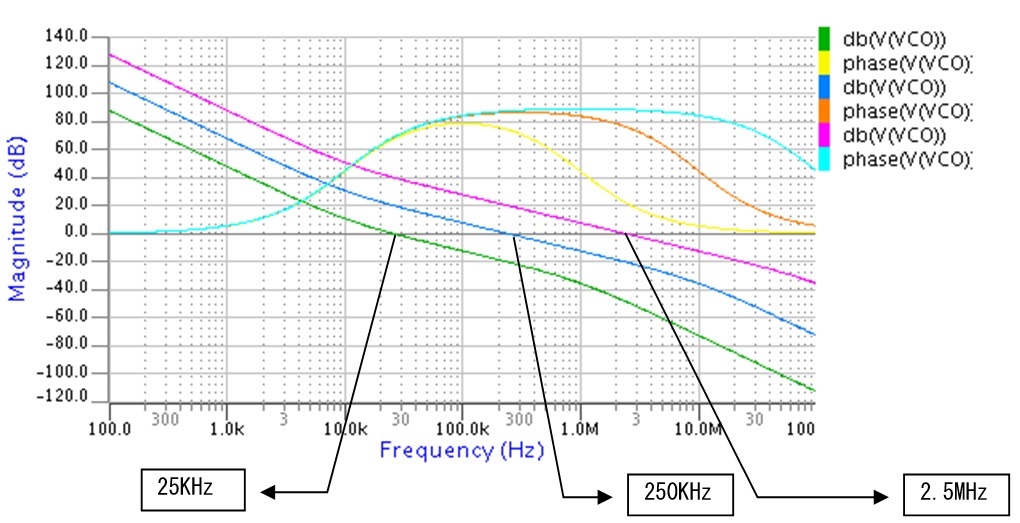
PLLの応答速度を、25KHz、250KHz、2.5MHzと変えたときにジッタ(つまり、V(PH)の動き)がどのように変化するかを見てみましょう。なお、それぞれのPLLの定数は以下の通りです。
PLLの応答速度=25KHzの時
25KHz
.param c1=160p r2=1k
.param c0=160n r0=100k r1=100
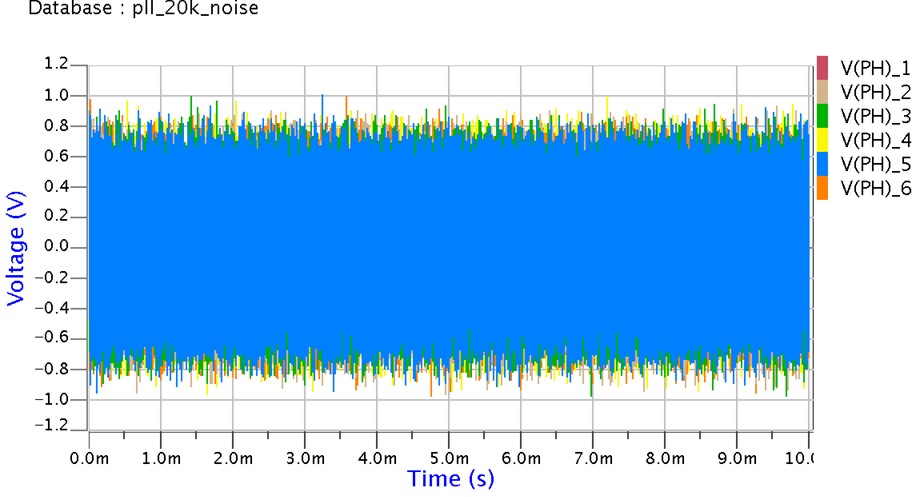
PLLがCLOSEに成ったので、ゆらゆらゆれている様子はなくなりましがが、V(PH):位相比較器の出力電圧が±1近くまで触れているので1周期近い位相雑音、つまりジッタが出ていることに成ります。
PLLの応答速度=250KHzの時
250KHz
.param c1=16p r2=1k
.param c0=16n r0=100k r1=1k
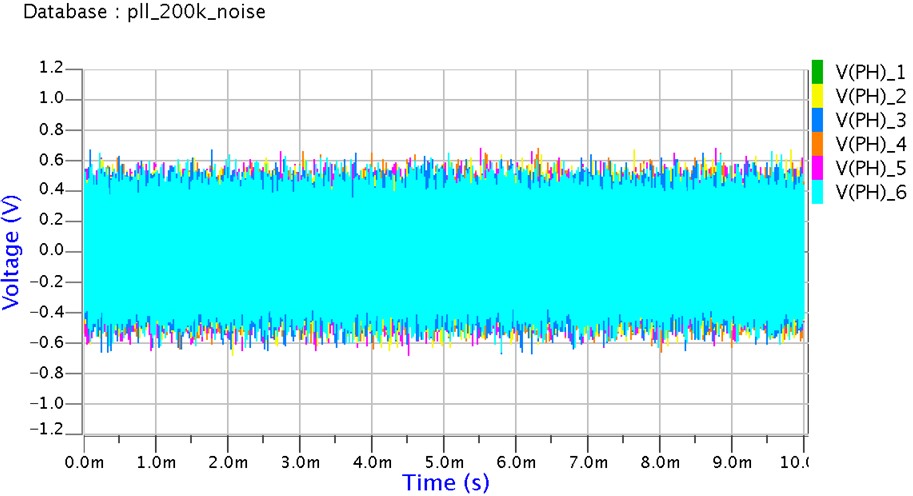
PLLの応答速度を早くすることで、だいぶ良くなりましたがまだ1周期の半分くらいのジッタが出ています。
PLLの応答速度=2.5MHzの時
2.5MHz
.param c1=1.6p r2=1k
.param c0=1.6n r0=100k r1=10k
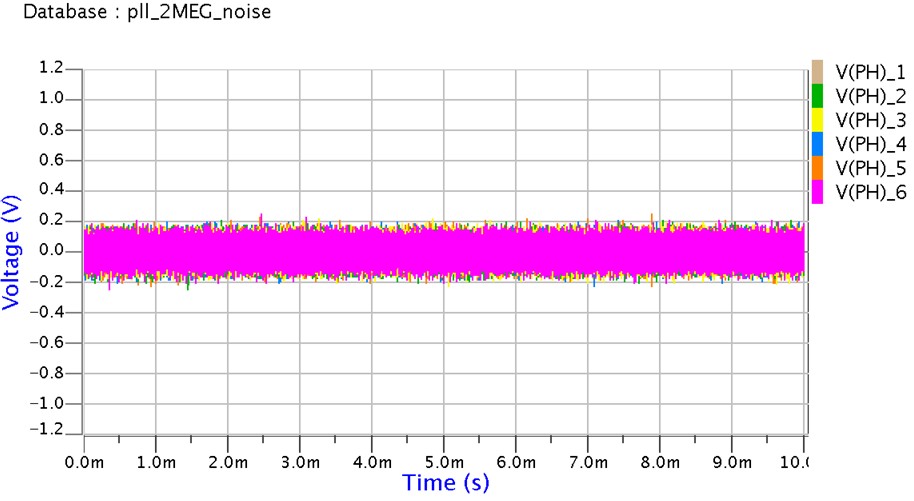
1周期の20%くらいのジッタになりましたので、これならクロックとして使えそうです。
PLLエラーアンプ出力の動きを比較する
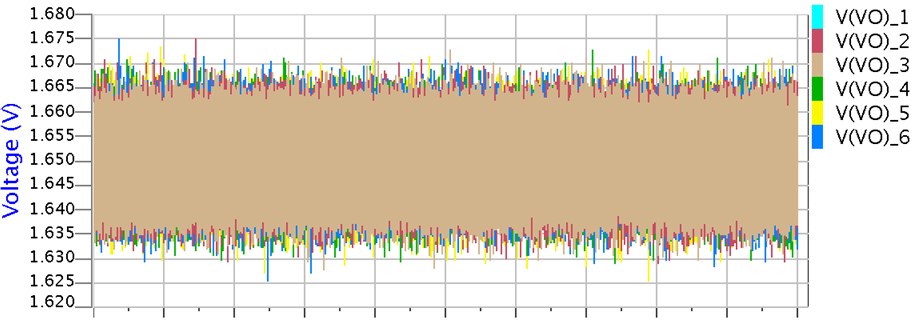
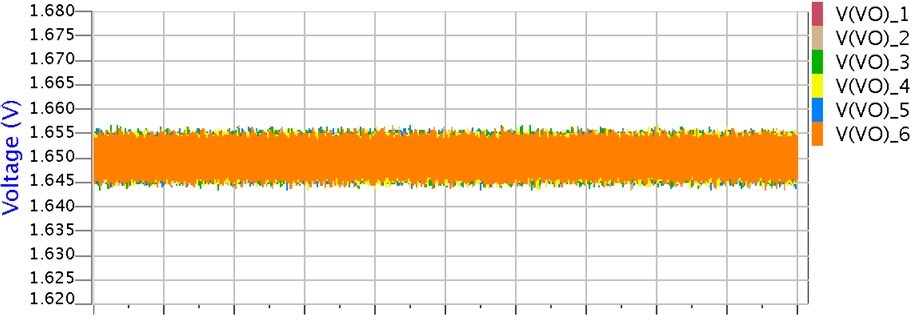
PLLのエラーアンプ出力(図 1のVo)の動きを比較してみると、次のようになります。
応答速度:25KHz
応答速度:2.5MHz
応答速度:250KHz
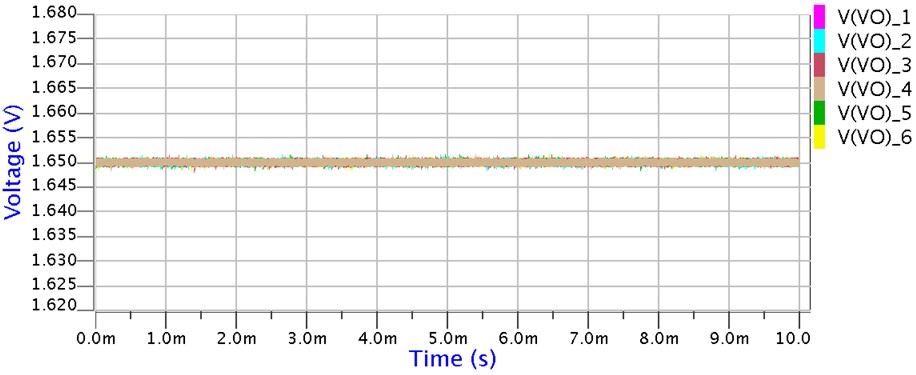
応答速度が速いほど、エラーアンプの出力電圧が活発に動きます・・・当たり前のことですが。
つまり応答速度が速いと、いち早くジッタを補正し、正しい位相にあわすことが出来るので、ジッタが少なくなるのです。
次回は・・・このまま雑音について話を進めたいと(今は)思っていますが、気が変わってしまうかもしれません。その時はご容赦下さい。
ではまた。
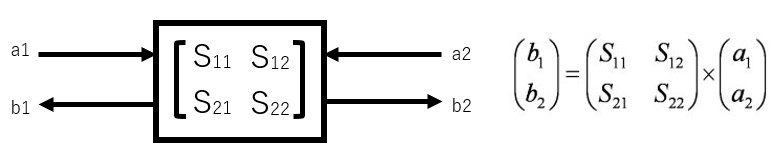
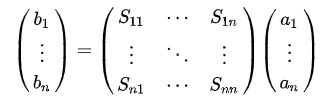
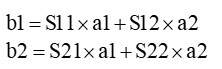
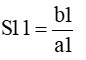 となって、反射係数と同じ計算式となります。つまり、
となって、反射係数と同じ計算式となります。つまり、